
※ C# Advent Calendar 2015 の12月19日の記事。
- 前の日の記事: 真・Roslyn for Scripting! あなたのアプリケーションにもC#スクリプトを!! - kekyoの丼
- 次の日の記事: Code整形でちょっと役立つCodeMaidの利用方法
C 等を使用している場合と異なり、C# では、それがメモリ上でどのような姿をしているのかを意識する機会は少なめだ。
C の場合、型とメモリ上のビットの並びを意識したプログラミングをする機会が多い。ビット演算も比較的良く使われる。 それに比べると、C# や Java などの言語だけを使っている場合は、そうした機会は割と少ない。
しかし、C# 等であっても、やはりそれぞれの型がメモリ上でどのようにして値を保持しているかを知っていることが有効な場合がある。 例えば、double の演算では誤差が生じることが多いが、double の内部表現を知ることで、その理由も腑に落ちやすいだろう。
本記事では、敢えて C# の double (System.Double) の内部の表現に焦点を当ててみたい。 後ろの方では、double の内部を見るクラスなども紹介する。
※ C# 6.0 を使用。
double を足したり引いたりすると誤差が生じる
C# で double や float のような浮動小数点数型を扱う場合には、誤差に注意する必要がある。
次の例では、↑ボタンを押す度に数値に 0.1 を足し、↓ボタンを押す度に数値から 0.1 を引いているのだが、何度も↑ボタンや↓ボタンを押した結果、誤差が生じている。
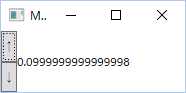
ちなみに、ソース コードは次のようなものだ。
UpDown.xaml.cs
using System.Windows; using System.Windows.Controls; namespace 浮動小数点数サンプル.WPF { public partial class UpDown : UserControl { const double d = 0.1; public static readonly DependencyProperty ValueProperty = DependencyProperty.Register("Value", typeof(double), typeof(UpDown), new PropertyMetadata(0.0)); public double Value { get { return (double)GetValue(ValueProperty); } set { SetValue(ValueProperty, value); } } public UpDown() { InitializeComponent(); } void OnUpButtonClick (object sender, RoutedEventArgs e) => Value += d; void OnDownButtonClick(object sender, RoutedEventArgs e) => Value -= d; } }
UpDown.xaml
<UserControl x:Class="浮動小数点数サンプル.WPF.UpDown" xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation" xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml" xmlns:mc="http://schemas.openxmlformats.org/markup-compatibility/2006" xmlns:d="http://schemas.microsoft.com/expression/blend/2008" xmlns:local="clr-namespace:浮動小数点数サンプル.WPF" mc:Ignorable="d" d:DesignHeight="80" d:DesignWidth="200"> <Grid> <Grid.RowDefinitions> <RowDefinition Height="*"/> <RowDefinition Height="*"/> </Grid.RowDefinitions> <Grid.ColumnDefinitions> <ColumnDefinition Width="Auto"/> <ColumnDefinition Width="Auto"/> </Grid.ColumnDefinitions> <RepeatButton Content="↑" Click="OnUpButtonClick"/> <RepeatButton Grid.Row="1" Content="↓" Click="OnDownButtonClick"/> <TextBlock Grid.Column="1" Grid.RowSpan="2" Text="{Binding Value, RelativeSource={RelativeSource FindAncestor, AncestorType={x:Type local:UpDown}}}" HorizontalAlignment="Right" VerticalAlignment="Center" TextWrapping="Wrap"/> </Grid> </UserControl>
問題点を絞るために、もっとシンプルなサンプルで見てみよう。
次の例では、コンソール アプリケーションで、0.1 を 20 回足した後に20回引いてみて、値の変化を表示している。
0.1 を 20 回足した後に20回引くコンソール アプリケーション
using System;
public static class Extension
{
// 回数繰り返す
public static void Repeat(this int times, Action action)
{
for (var counter = 0; counter < times; counter++)
action();
}
}
static class Program
{
static void WriteLine(double value) => Console.WriteLine($"{value:f16}");
static void Main()
{
// 0.0 から 0.1 ずつ20回増やしていき、0.1 ずつ20回減らしていく
const int times = 20;
const double d = 0.1;
double value = 0.0;
WriteLine(value);
times.Repeat(() => WriteLine(value += d));
times.Repeat(() => WriteLine(value -= d));
}
}
実行結果は次の通りだ。
最後の方で誤差が生じているのが分かる。
0.1 を 20 回足した後に20回引くコンソール アプリケーションの実行結果
0.0000000000000000
0.1000000000000000
0.2000000000000000
0.3000000000000000
0.4000000000000000
0.5000000000000000
0.6000000000000000
0.7000000000000000
0.8000000000000000
0.9000000000000000
1.0000000000000000
1.1000000000000000
1.2000000000000000
1.3000000000000000
1.4000000000000000
1.5000000000000000
1.6000000000000000
1.7000000000000000
1.8000000000000000
1.9000000000000000
2.0000000000000000
1.9000000000000000
1.8000000000000000
1.7000000000000000
1.6000000000000000
1.5000000000000000
1.4000000000000000
1.3000000000000000
1.2000000000000000
1.1000000000000000
1.0000000000000000
0.9000000000000000
0.8000000000000000
0.7000000000000000
0.6000000000000000
0.5000000000000000
0.4000000000000000
0.3000000000000000
0.2000000000000000
0.0999999999999998
-0.0000000000000002
どうしてこのような誤差が生じるのだろうか?
情報落ち
「情報落ち」と呼ばれる現象がある。
絶対値が大きな値と小さな値を足したり引いたりした場合、小さい方の数値の末尾の分の情報が失われる、というものだ。
例えば、十進数で 1111111111.11111 と 1.11111111112345 を足す場合を考えてみよう。 double の有効桁は十進数で15桁程度なので、そうした場合を想定してみる。
有効桁が15桁の場合、1111111111.11111 + 1.11111111112345 = 1111111112.22222 となり、足し算の結果が小さい方の数値の末尾の分小さくなっている。 このような演算を繰り返すと、どんどんこの分の誤差が積もっていくことになる。
今回の場合だが、果たして 0.1 を足したり引いたりするだけで、このような誤差が生じるのだろうか。 0.1 の足し算や引き算であれば、有効桁が15桁もあれば誤差は生じないのではなかろうか。
その鍵は、double の内部表現にある。
二進数としての小数
double の内部表現は二進数である。
そこで、二進数としての小数を考えてみよう。
例えば、十進数で 2.5 の場合、これを二進数で表現すると次のようになる。
2.5(10) = 2 + 0.5 = 10(2) + 1×2-1 = 10.1(2)
そして、十進数で 0.1 の場合、二進数で表現すると、次のように循環小数となるのだ。
0.1(10) = 0.0 0011 0011 0011…(2)
double 内部の二進数としての有効桁は、52 + 1桁である。十進数としての 0.1 を入れたつもりでも、実際には循環小数の全ての桁を格納できる訳ではないので、有効桁を超えた分の情報はなくなってしまい、僅かに 0.1 と異なる値が格納されることになる。
また、この場合、有効桁いっぱいまで使って 0.1 に近い値を表現しているので、絶対値がより大きい値との演算で情報落ちが起こることがある。
double の内部表現
では、double の内部表現をもっと詳しくみてみよう。
double は、次のような構造をしている。これは、「IEEE 754 倍精度 浮動小数点形式」と呼ばれる形式だ。

64ビットの中に二進数で、 符号部、指数部、仮数部の三つが格納されており、次のような値を表す。
| 部分 | ビット数 | 意味 | 補足 |
|---|---|---|---|
| 符号部 | 1 ビット | 負の数かどうかを表す | 1: 負の数、0: 負の数ではない |
| 指数部 | 11 ビット | 指数 | 1023 足される |
| 仮数部 | 52 ビット | 仮数の絶対値 | 非 0 の場合 1.XXXXX… になるように指数部で調整され、最上位の 1 は省かれる |
例えば、2.5(10) の場合だと次のようになる:
2.5(10)
= 10.1(2)
= 10.1(2)×20
= 1.01(2)×21 (1.XXXXX… になるように調整)
そして、それぞれの部分は次のようになる。
| 部分 | 値 | 補足 |
|---|---|---|
| 符号部 | 0 | 負の数でない |
| 指数部 | 10000000000 | 1(10)+1023(10)=1024(10)=10000000000(2) |
| 仮数部 | 0100000000000000000000000000000000000000000000000000 | 1.0100000000000000000000000000000000000000000000000000 の先頭の 1. を省いたもの |
従って、2.5(10) を double に格納したときの全体の内部表現は、|0|10000000000|0100000000000000000000000000000000000000000000000000| となる。
そして、0.1(10) の場合だと次のようになる:
0.1(10)
= 0.0 0011 0011 0011 …(2) (循環小数となる)
= 1.1 0011 0011 …(2) × 2-4 (1.XXXXX… になるように調整)
それぞれの部分は次のようになる。
| 部分 | 値 | 補足 |
|---|---|---|
| 符号部 | 0 | 負の数でない |
| 指数部 | 01111111011 | -4(10)+1023(10)=1019(10)=01111111011(2) |
| 仮数部 | 1001100110011001100110011001100110011001100110011010 | 1.1 0011 0011 …(2) の整数部分の1を省略し、最後の桁の次の桁を「0捨1入」 |
つまり、0.1(10) を double に格納したときの全体の内部表現は、|0|01111111011|1001100110011001100110011001100110011001100110011010| となる。
尚、同じく浮動小数点数型である float に関しても同様だ。こちらは、4 バイト = 32 ビット (符号部 1 ビット、指数部 8 ビット、仮数部 23 ビット) となる。
C# で double の内部の値を見てみよう
最後に、C# で double の内部の値を見るクラスを作ってみよう。
先ず、double をバイト列にしたり、バイト列を十六進数表現に変換したり、十六進数表現を二進数表現に変換したりするメソッド群を用意した。
バイト列に変換するのには、System.BitConverter クラスが使用できる。 また、メモリ上での配置がリトル エンディアンになっている場合は、反転する必要があるが、これも System.BitConverter クラスで判定できる。
十六進数や二進数としての表現は、文字列として得られるようにした。
BinaryUtility.cs
using System; using System.Linq; using System.Text; public static class BinaryUtility { // バイト列をビッグ エンディアンに変換 (メモリ上での配置がリトル エンディアンになっている場合は反転) public static byte[] ToBigEndian(this byte[] bytes) => BitConverter.IsLittleEndian ? bytes.Reverse().ToArray() : bytes; // double をバイト列に変換 (ビッグ エンディアン) public static byte[] ToBytes(this double value) => BitConverter.GetBytes(value).ToBigEndian(); // バイト列を十六進数に変換 public static string ToHexadecimalNumber(this byte[] byteArray) => BitConverter.ToString(byteArray).Replace("-", ""); // 十六進数一桁を二進数に変換 public static string HexadecimalNumberToBinaryNumber(char hexadecimalNumber) => Convert.ToString(Convert.ToInt32(hexadecimalNumber.ToString(), 16), 2).PadLeft(4, '0'); // 十六進数を二進数に変換 public static string HexadecimalNumberToBinaryNumber(string hexadecimalString) => hexadecimalString.Select(character => HexadecimalNumberToBinaryNumber(character)) .Aggregate(new StringBuilder(), (stringBuilder, text) => stringBuilder.Append(text)) .ToString(); // 二進数一桁を int に変換 public static int BinaryNumberToInteger(char binaryNumber) => binaryNumber == '0' ? 0 : 1; }
次に、これを利用して、double 即ち IEEE 754 倍精度 浮動小数点形式から各部分の値を取り出すクラスを作ってみよう。
IEEE754Double.cs
using System; // IEEE 754 倍精度 浮動小数点形式 (8バイト) // 符号部 1bit マイナス符号があるとき1 // 指数部 11bits 指数 + 2^10−1 (2^10−1 = 1024 - 1 = 1023) // 仮数部 52bits 整数部分の1を省略 // ※ 仮数部は整数部分が1のみになるように調整 public class IEEE754Double { const int exponentBias = 1024 - 1; // 指数のバイアス: 2^10−1 = 1024 - 1 = 1023 readonly double value; // double としての値 readonly string hexadecimalNumber; // 十六進数 readonly string binaryNumber; // ニ進数 public IEEE754Double(double value) { this.value = value; hexadecimalNumber = value.ToBytes().ToHexadecimalNumber(); binaryNumber = BinaryUtility.HexadecimalNumberToBinaryNumber(HexadecimalNumber); } // double としての値 public double Value => value; // 十六進数 public string HexadecimalNumber => hexadecimalNumber; // ニ進数 public string BinaryNumber => binaryNumber; // 符号部の二進数 (マイナス符号があるかないか: 符号部 1bit) public char SignBinaryNumber => binaryNumber[0]; // 指数部の二進数 (指数部 11bits) public string ExponentBinaryNumber => binaryNumber.Substring(1, 11); // 仮数部の二進数 (仮数部 52bits : 整数部分の1を省略した小数部分) public string DigitsBinaryNumber => binaryNumber.Substring(1 + 11, 64 - 1 - 11); // 符号 (マイナス符号があるかないか: 符号部 1bit から取得) public bool Sign => SignBinaryNumber == '1'; // 指数 (「指数部 11bits: 指数 + 指数のバイアス」から取得) public int Exponent => Convert.ToInt32(ExponentBinaryNumber, 2) - exponentBias; // 仮数 public double Digits { get { var wholeDigitsBinaryNumber = "1" + DigitsBinaryNumber; // 二進数 // 二進数を double に変換 var result = 0.0; for (var index = wholeDigitsBinaryNumber.Length - 1; index >= 0; index--) result = result / 2.0 + BinaryUtility.BinaryNumberToInteger(wholeDigitsBinaryNumber[index]); return result; } } public override string ToString() => $"{SignString}{Digits} * 2^{Exponent}"; // 符号文字列 (- または +) string SignString => Sign ? "-" : "+"; }
これらを使って、2.5(10) と 0.1(10) の内部の値をみてみよう。
Program.cs
using System;
static class Program
{
static void WriteLine(double value)
{
var i3eDouble = new IEEE754Double(value);
Console.WriteLine($"{i3eDouble.Value:f16}, {i3eDouble.HexadecimalNumber}, {i3eDouble.BinaryNumber}, {i3eDouble.ToString()}");
}
static void Main()
{
WriteLine(2.5);
WriteLine(0.1);
}
}
実行結果は次のようになる。 先に考察したのと同じ結果だ。
2.5000000000000000, 4004000000000000, 0100000000000100000000000000000000000000000000000000000000000000, +1.25 * 2^1
0.1000000000000000, 3FB999999999999A, 0011111110111001100110011001100110011001100110011001100110011010, +1.6 * 2^-4
試しに、double.MaxValue、double.MinValue、double.PositiveInfinity、double.NegativeInfinity、double.NaN を出してみると次のようになった。
179769313486232000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000.0000000000000000, 7FEFFFFFFFFFFFFF, 0111111111101111111111111111111111111111111111111111111111111111, +2 * 2^1023
-179769313486232000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000.0000000000000000, FFEFFFFFFFFFFFFF, 1111111111101111111111111111111111111111111111111111111111111111, -2 * 2^1023
∞, 7FF0000000000000, 0111111111110000000000000000000000000000000000000000000000000000, +1 * 2^1024
-∞, FFF0000000000000, 1111111111110000000000000000000000000000000000000000000000000000, -1 * 2^1024
NaN, FFF8000000000000, 1111111111111000000000000000000000000000000000000000000000000000, -1.5 * 2^1024
double.PositiveInfinity、double.NegativeInfinity、double.NaN に関しては最後の部分は無用だが、それぞれの内部表現は確認できた。
では、始めの方で行った、0.1 を足したり引いたりする例について試してみよう。
Program.cs
using System;
public static class Extension
{
// 回数繰り返す
public static void Repeat(this int times, Action action)
{
for (var counter = 0; counter < times; counter++)
action();
}
}
static class Program
{
static void WriteLine(double value)
{
var i3eDouble = new IEEE754Double(value);
Console.WriteLine($"{i3eDouble.Value:f16}, {i3eDouble.HexadecimalNumber}, {i3eDouble.BinaryNumber}, {i3eDouble.ToString()}");
}
static void Main()
{
// 0.0 から 0.1 ずつ20回増やしていき、0.1 ずつ20回減らしていく
const int times = 20;
const double d = 0.1;
double value = 0.0;
WriteLine(value);
times.Repeat(() => WriteLine(value += d));
times.Repeat(() => WriteLine(value -= d));
}
}
実行結果は次のようになった。 二進数の演算で誤差が生じている箇所が確認できるだろうか。
0.0000000000000000, 0000000000000000, 0000000000000000000000000000000000000000000000000000000000000000, +1 * 2^-1023
0.1000000000000000, 3FB999999999999A, 0011111110111001100110011001100110011001100110011001100110011010, +1.6 * 2^-4
0.2000000000000000, 3FC999999999999A, 0011111111001001100110011001100110011001100110011001100110011010, +1.6 * 2^-3
0.3000000000000000, 3FD3333333333334, 0011111111010011001100110011001100110011001100110011001100110100, +1.2 * 2^-2
0.4000000000000000, 3FD999999999999A, 0011111111011001100110011001100110011001100110011001100110011010, +1.6 * 2^-2
0.5000000000000000, 3FE0000000000000, 0011111111100000000000000000000000000000000000000000000000000000, +1 * 2^-1
0.6000000000000000, 3FE3333333333333, 0011111111100011001100110011001100110011001100110011001100110011, +1.2 * 2^-1
0.7000000000000000, 3FE6666666666666, 0011111111100110011001100110011001100110011001100110011001100110, +1.4 * 2^-1
0.8000000000000000, 3FE9999999999999, 0011111111101001100110011001100110011001100110011001100110011001, +1.6 * 2^-1
0.9000000000000000, 3FECCCCCCCCCCCCC, 0011111111101100110011001100110011001100110011001100110011001100, +1.8 * 2^-1
1.0000000000000000, 3FEFFFFFFFFFFFFF, 0011111111101111111111111111111111111111111111111111111111111111, +2 * 2^-1
1.1000000000000000, 3FF1999999999999, 0011111111110001100110011001100110011001100110011001100110011001, +1.1 * 2^0
1.2000000000000000, 3FF3333333333333, 0011111111110011001100110011001100110011001100110011001100110011, +1.2 * 2^0
1.3000000000000000, 3FF4CCCCCCCCCCCD, 0011111111110100110011001100110011001100110011001100110011001101, +1.3 * 2^0
1.4000000000000000, 3FF6666666666667, 0011111111110110011001100110011001100110011001100110011001100111, +1.4 * 2^0
1.5000000000000000, 3FF8000000000001, 0011111111111000000000000000000000000000000000000000000000000001, +1.5 * 2^0
1.6000000000000000, 3FF999999999999B, 0011111111111001100110011001100110011001100110011001100110011011, +1.6 * 2^0
1.7000000000000000, 3FFB333333333335, 0011111111111011001100110011001100110011001100110011001100110101, +1.7 * 2^0
1.8000000000000000, 3FFCCCCCCCCCCCCF, 0011111111111100110011001100110011001100110011001100110011001111, +1.8 * 2^0
1.9000000000000000, 3FFE666666666669, 0011111111111110011001100110011001100110011001100110011001101001, +1.9 * 2^0
2.0000000000000000, 4000000000000001, 0100000000000000000000000000000000000000000000000000000000000001, +1 * 2^1
1.9000000000000000, 3FFE666666666668, 0011111111111110011001100110011001100110011001100110011001101000, +1.9 * 2^0
1.8000000000000000, 3FFCCCCCCCCCCCCE, 0011111111111100110011001100110011001100110011001100110011001110, +1.8 * 2^0
1.7000000000000000, 3FFB333333333334, 0011111111111011001100110011001100110011001100110011001100110100, +1.7 * 2^0
1.6000000000000000, 3FF999999999999A, 0011111111111001100110011001100110011001100110011001100110011010, +1.6 * 2^0
1.5000000000000000, 3FF8000000000000, 0011111111111000000000000000000000000000000000000000000000000000, +1.5 * 2^0
1.4000000000000000, 3FF6666666666666, 0011111111110110011001100110011001100110011001100110011001100110, +1.4 * 2^0
1.3000000000000000, 3FF4CCCCCCCCCCCC, 0011111111110100110011001100110011001100110011001100110011001100, +1.3 * 2^0
1.2000000000000000, 3FF3333333333332, 0011111111110011001100110011001100110011001100110011001100110010, +1.2 * 2^0
1.1000000000000000, 3FF1999999999998, 0011111111110001100110011001100110011001100110011001100110011000, +1.1 * 2^0
1.0000000000000000, 3FEFFFFFFFFFFFFD, 0011111111101111111111111111111111111111111111111111111111111101, +2 * 2^-1
0.9000000000000000, 3FECCCCCCCCCCCCA, 0011111111101100110011001100110011001100110011001100110011001010, +1.8 * 2^-1
0.8000000000000000, 3FE9999999999997, 0011111111101001100110011001100110011001100110011001100110010111, +1.6 * 2^-1
0.7000000000000000, 3FE6666666666664, 0011111111100110011001100110011001100110011001100110011001100100, +1.4 * 2^-1
0.6000000000000000, 3FE3333333333331, 0011111111100011001100110011001100110011001100110011001100110001, +1.2 * 2^-1
0.5000000000000000, 3FDFFFFFFFFFFFFC, 0011111111011111111111111111111111111111111111111111111111111100, +2 * 2^-2
0.4000000000000000, 3FD9999999999996, 0011111111011001100110011001100110011001100110011001100110010110, +1.6 * 2^-2
0.3000000000000000, 3FD3333333333330, 0011111111010011001100110011001100110011001100110011001100110000, +1.2 * 2^-2
0.2000000000000000, 3FC9999999999993, 0011111111001001100110011001100110011001100110011001100110010011, +1.6 * 2^-3
0.0999999999999998, 3FB999999999998C, 0011111110111001100110011001100110011001100110011001100110001100, +1.6 * 2^-4
-0.0000000000000002, BCAC000000000000, 1011110010101100000000000000000000000000000000000000000000000000, -1.75 * 2^-53
まとめ
以上、double の内部表現について、C# を使って説明してみた。